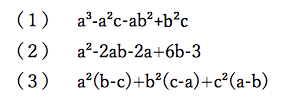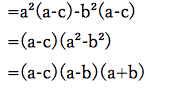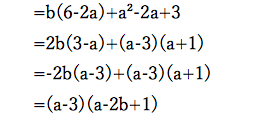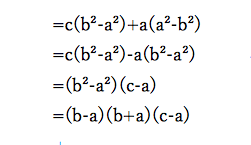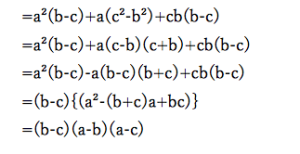こんにちは。千石教室の南です。
4月に入りました。
新学年が始まるということで皆さんウキウキしていると思います。
ただ一方で、これまでと比べて勉強が難しくなり、アタフタするのがこの4、5月の恒例行事です。
私個人的には中3、高1の因数分解でえらい苦戦した記憶があります。
基本的な問題のうちはよかったのですが、難解なものになると手が止まるわけです。
授業中にも繰り返しお伝えしていますが、今回は因数分解に意識するべきテクニックを2つお伝えしたいと思います。
まず、下の問題を見てみましょう
いかがでしょうか。
1問目はできた人が多いと思います。試行錯誤していけば(a−c)という因数を見つけられると思います。前の2項をaの2乗でくくってしまえばいいわけですね。
さてここで私は授業中に口酸っぱく言っているのですが、
「難問になると勘頼みで試行錯誤しても、解けない場合が多い」のです。
そのため、確信的にどうやって因数を見つけられるかの戦略を意識する必要があります。
例えば(2)です。
この問題の場合は、項が5つもありますから、 (1)のように盲目的にやっていると、どの因数でくくればいいのか分かるには時間がかかりませんか?
ここで覚えておいて欲しいテクニック1つ目は
「字数の低い文字について整理する!」というテクニックです。
この問題であればaは2次、bは1次ですから、bについて整理すればいいと確信的に分かるのです。
ちなみに(1)についてテクニック通りに解くと以下のような計算過程を辿ります。
初めに記した解法とは異なることがわかります。
生徒が書いた式を見ると、盲目的に解いたのか、戦略を持ってといたかが一目瞭然にわかります。
さて、(3)を見てみましょう。
さすがにこの問題は試行錯誤しても解けませんね。
でテクニック一つ目を実行するのですが、aもbもcもすべて2次です。
というわけで一つ目のテクニックは使えません。
そういう場合に使うテクニック2つ目は
「字数が同じ場合は、どの文字でもいいので、ある文字で降べきの順に整理する」のです。
今回はaに注目してaの二次式として整理しましょう。
学年があがるほど、「なんとなく因数分解できる」という機会は減っていきます。
むしろ確信を持って式・項を整理しないと因数分解できなくなってきます。
再度言いますが、
①「字数の低い文字について整理する!」
②「字数が同じ場合は、どの文字でもいいので、ある文字で降べきの順に整理する」
勘頼みのなんとなくの因数分解から、確信的な因数分解ができるよう努めてください。