千石教室の佐藤です。
先日、数珠順列について生徒から質問がありましたので今回は数珠順列の正しい考え方について書きたいと思います。
数珠順列というと、公式【 (n-1)!/2 】で計算すればいいと思っている生徒がほとんどですが、実はその考え方はやめた方がいいです。
円順列をただ2で割ればいいという考え方は間違いです。
例えば、
ガラスの玉で赤色が6個、青色が2個、透明が1個ある。首飾りを作る方法は何通りか。という問題。
これらを円形に並べる方法は28通りです。
それを2で割って14通りとする誤りが後を絶ちません。
では、どのように考えればよいのか。
数珠順列では、円順列の中で①左右対称なものと②左右非対称なものに場合分けして考えてください。
円順列の28通りのうち、
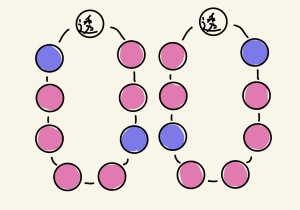
①左右対称なものは次の4通り。
この4通りは全て異なる首輪となる。
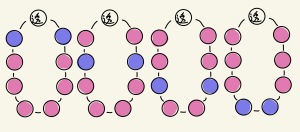
②28通りのうち、左右対称でないものは、28−4=24通り。
このうち、2つ例を挙げると、
上2つは同じ首輪。裏返すと同じ。
よって24/2=12通り。
したがって、4+12=16
16通りの首輪ができる。
このように、数珠順列では、円順列の中で①左右対称なものと②左右非対称なものに場合分けして考えるようにしましょう。
ーー体験授業は随時受付していますーーー
【千石教室】
文京区千石1丁目15-5 千石文化苑ビル3階
TEL:03-6902-1980(受付16:00~21:30)
【西ケ原教室】
北区西ケ原1丁目30-1 東高西ケ原ペアシティ1階
TEL:03-6903-5760(受付16:00~21:30)