フレック学習塾数学担当の佐藤です。
本日実施された2026年度都立高校入試。
数学は大問1~4までは例年通り、最後の空間図形で難化という構成でした。
全体としては例年通り「基礎の完成度」が問われる試験です。
ただし、大問5で差がついた可能性が高いです。
【大問1】小問集合(難易度★)
例年通りの頻出パターン。
- 計算
- 方程式
- 円周角
- 作図(回転移動)
回転移動の作図も標準的。
特別なひねりはなく、教科書レベルの理解で十分対応可能でした。
ここは満点を取りたい大問。
1問(5点)でも落とした場合は大ダメージ。

【大問2】数の性質(難易度★)
2桁・3桁の自然数を文字で表す問題。
例)
- 2桁の整数 → 10a+b
- 3桁の整数 → 100a+10b+c
典型問題です。
読解力問題、状況を整理できればスムーズに立式できる内容でした。
焦らず処理できたかどうかがポイントです。

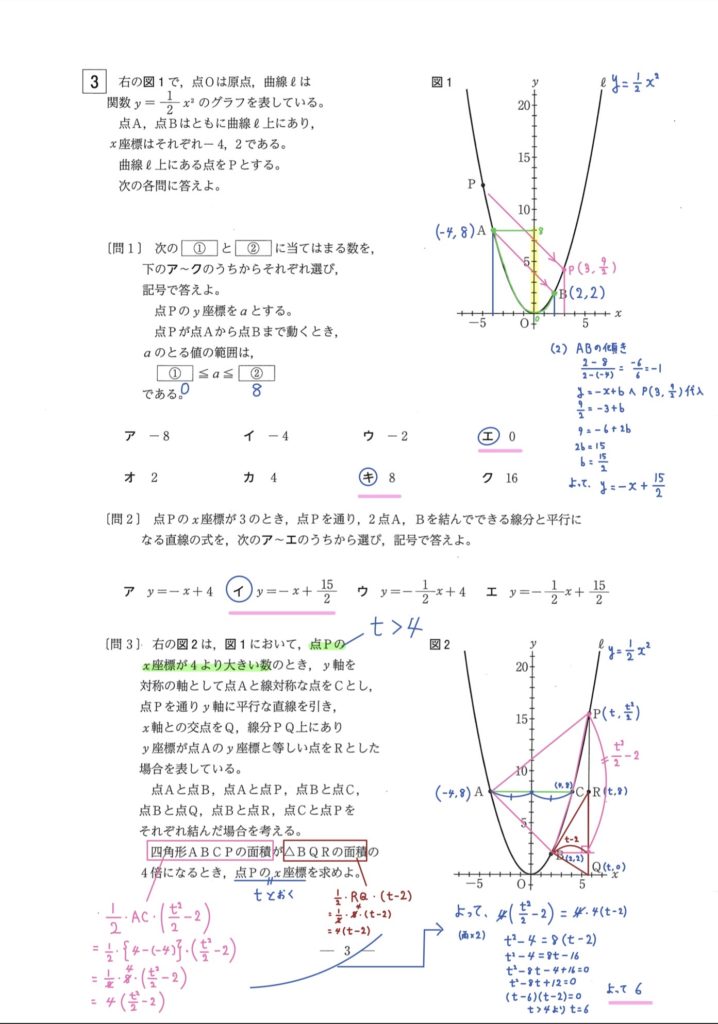
【大問3】関数(難易度★★)
- 1次関数の一般形を利用
- 2次関数のグラフと図形
点Pのx座標を文字で置き、図形の関係から式を立てて求める典型問題。
都立対策では王道中の王道です。
フレック学習塾では、V模擬レベルの2次関数融合問題を徹底的に山程演習してきました。
正直に言えば――
フレック学習塾の生徒にとっては【差がつく問題】ではなく、【差をつける問題】。
演習量は裏切りません。
大問3は、その成果がはっきり出る問題でした。
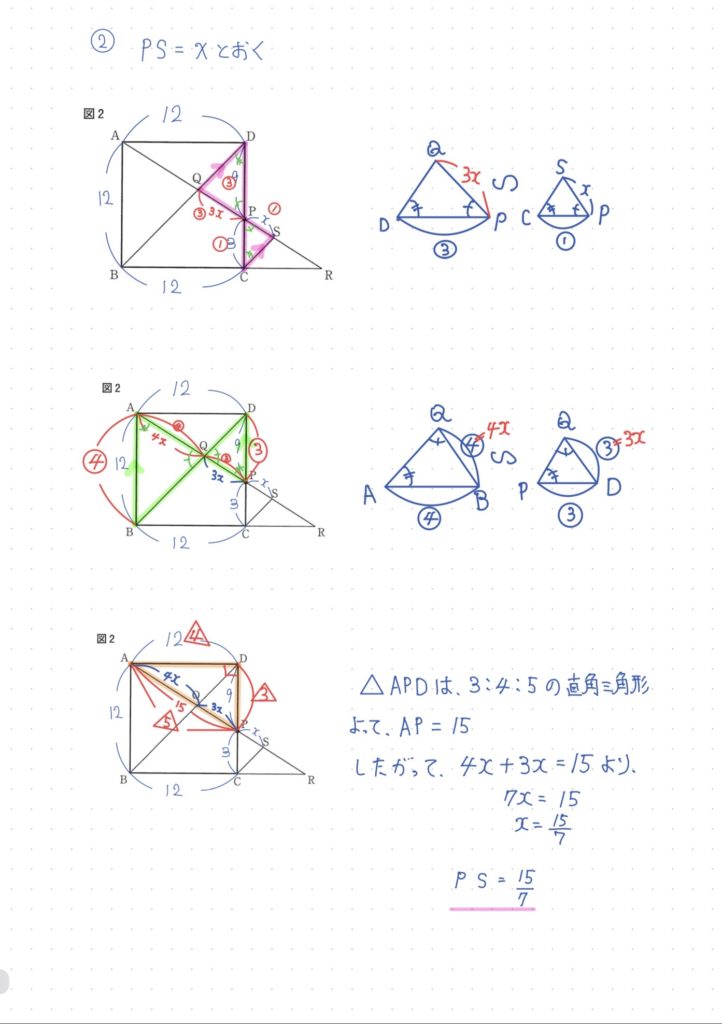
【大問4】平面図形(難易度★★★)
角度、相似の証明、相似を用いた線分の長さ。
いずれも都立の王道パターンでした。
最後は、いわゆる『砂時計を探しまくる問題』
どこに相似が潜んでいるかを見抜けるかどうかが勝負です。
フレック学習塾では、V模擬レベルの相似演習を徹底的に反復。
砂時計型は【見つけるもの】ではなく、【見えるもの】にしてきました。
今回の大問4も、
フレック学習塾の生徒にとっては完答前提の得点源。
ここで取り切れるかどうかが、準備量の差です。
AR上を比で分けて考える解法(王道パターン)で解いた生徒も多いと思います。
解法パターンが様々考えられますが今回は以下の解法が最短ルート。

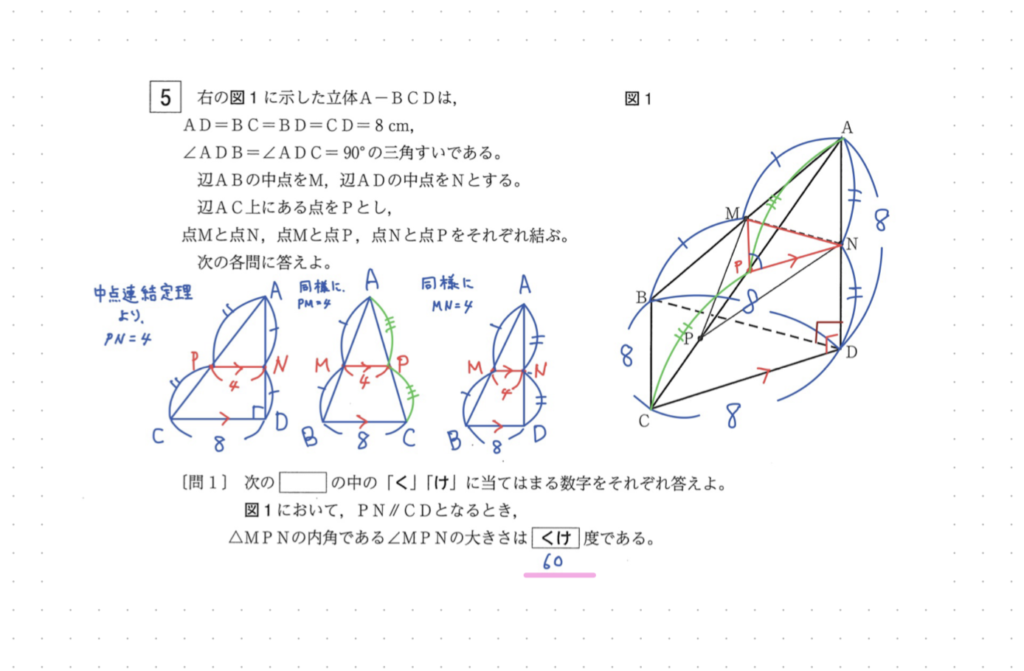
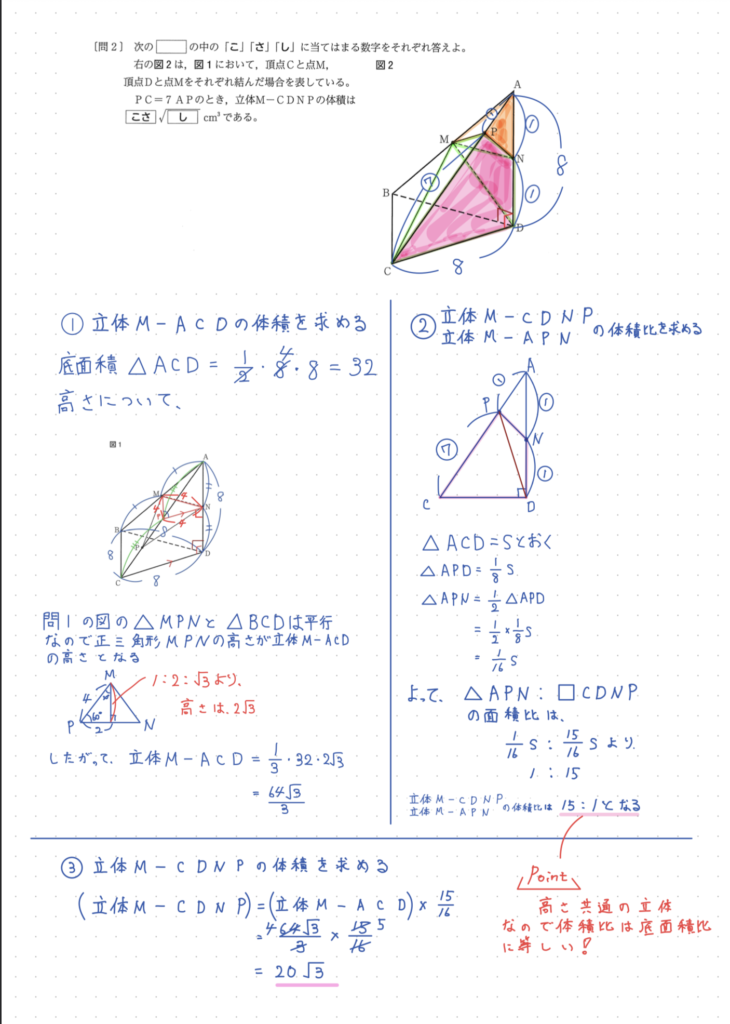
【大問5】空間図形(難易度★★★★★)
今年の山場。
- 問1:角度 (中点連結定理利用)
- 問2:体積
解法は複数ありますが、
立体の切断や比の扱いに慣れていないと厳しい内容。
昨年度と比較すると明らかに難化。
時間配分を誤るとここで崩れます。
正答率はかなり低いと予想されます。
都立数学は毎年、「難問を解けるか」ではなく「取るべき問題を落とさないか」
が合否を分けます。今年は特にそれが顕著でした。
2027年度受験生へ
・小問集合は絶対落とさない。
・関数は文字で置く勇気をつける。
・空間図形は、逃げずに考え抜くしかない。
そして
・相似は『砂時計を探しまくれ』見つけた人が勝ち。
都立数学は、準備量の勝負。
来年、この問題を
【見たことある】に変えられるかどうか。
それは、これからの一年で決まります。
============== 体験授業、随時受付中 ======================
【フレック学習塾 西ケ原教室】
西ヶ原、駒込、上中里から通塾可能
北区西ケ原1丁目30-1 東高西ケ原ペアシティ1階
TEL:03-6903-5760(受付16:00~21:00)
【フレック学習塾 千石教室】
千石、巣鴨、白山から通塾可能
文京区千石1丁目15-5 千石文化苑ビル3階
TEL:03-6902-1980(受付16:00~21:00)




